Following are scalar moments of inertia. In general, the moment of inertia is a tensor, see below.
Description
Figure
Moment(s) of inertia
Point mass m at a distance r from the axis of rotation. A point mass does not have a moment of inertia around its own axis, but using the parallel axis theorem a moment of inertia around a distant axis of rotation is achieved.

Two point masses, M and m, with reduced mass μ and separated by a distance, x.

Rod of length L and mass m, axis of rotation at the end of the rod. This expression assumes that the rod is an infinitely thin (but rigid) wire. This is also a special case of the thin rectangular plate with axis of rotation at the end of the plate, with h = L and w = 0.

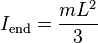 [1]
[1]
Rod of length L and mass m. This expression assumes that the rod is an infinitely thin (but rigid) wire. This is a special case of the thin rectangular plate with axis of rotation at the center of the plate, with w = L and h = 0.

 [1]
[1]
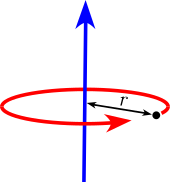
Thin circular hoop of radius r and mass m. This is a special case of a torus for b = 0 (see below), as well as of a thick-walled cylindrical tube with open ends, with r1 = r2 and h = 0.



Thin, solid disk of radius r and mass m. This is a special case of the solid cylinder, with h = 0. That is a consequence of the Perpendicular axis theorem.
is a consequence of the Perpendicular axis theorem.

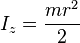

Thin cylindrical shell with open ends, of radius r and mass m. This expression assumes that the shell thickness is negligible. It is a special case of the thick-walled cylindrical tube for r1 = r2.
Also, a point mass m at the end of a rod of length r has this same moment of inertia and the value r is called the radius of gyration.

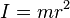 [1]
[1]
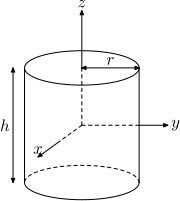
Solid cylinder of radius r, height h and mass m.
This is a special case of the thick-walled cylindrical tube, with r1 = 0. (Note: X-Y axis should be swapped for a standard right handed frame).

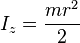 [1]
[1]
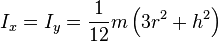
Thick-walled cylindrical tube with open ends, of inner radius r1, outer radius r2, length h and mass m. With a density of ρ and the same geometry ,
, 

 [1] [2]
[1] [2]
where t = (r2–r1)/r2 is a normalized thickness ratio;
![I_x = I_y = \frac{1}{12} m\left[3\left({r_2}^2 + {r_1}^2\right)+h^2\right]](http://upload.wikimedia.org/math/3/b/2/3b287e5226f4bb01de7a7a3066f4202a.png)
Tetrahedron of side s and mass m


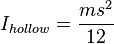
Octahedron (hollow) of side s and mass m


Octahedron (solid) of side s and mass m


Sphere (hollow) of radius r and mass m. A hollow sphere can be taken to be made up of two stacks of infinitesimally thin, circular hoops, where the radius differs from 0 to r (or a single stack, where the radius differs from -r to r).

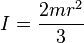 [1]
[1]
Ball (solid) of radius r and mass m. A sphere can be taken to be made up of two stacks of infinitesimally thin, solid discs, where the radius differs from 0 to r (or a single stack, where the radius differs from -r to r).

 [1]
[1]
Sphere (shell) of radius r2, with centered spherical cavity of radius r1 and mass m. When the cavity radius r1 = 0, the object is a solid ball (above).
When r1 = r2,![\left[\frac{{r_2}^5-{r_1}^5}{{r_2}^3-{r_1}^3}\right]=\frac{5}{3}{r_2}^2](http://upload.wikimedia.org/math/d/5/7/d57cd8acd84d2fac233b03050dd61fac.png) , and the object is a hollow sphere.
, and the object is a hollow sphere.

![I = \frac{2 m}{5}\left[\frac{{r_2}^5-{r_1}^5}{{r_2}^3-{r_1}^3}\right]\,\!](http://upload.wikimedia.org/math/d/7/3/d7341dbed710e5dd97ef720c6f2582db.png) [1]
[1]
Right circular cone with radius r, height h and mass m

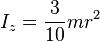 [3]
[3]
 [3]
[3]
Torus of tube radius a, cross-sectional radius b and mass m.

About the vertical axis: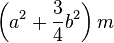 [4]
[4]
About a diameter: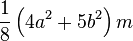 [4]
[4]
Ellipsoid (solid) of semiaxes a, b, and c with mass m




Thin rectangular plate of height h, width w and mass m
(Axis of rotation at the end of the plate)


Thin rectangular plate of height h and of width w and mass m

 [1]
[1]
Solid cuboid of height h, width w, and depth d, and mass m. For a similarly oriented cube with sides of length ,
, 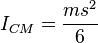

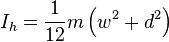
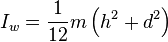
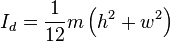
Solid cuboid of height D, width W, and length L, and mass m with the longest diagonal as the axis. For a cube with sides ,
,  .
.


Triangle with vertices at the origin and at P and Q, with mass m, rotating about an axis perpendicular to the plane and passing through the origin.

Plane polygon with vertices P1, P2, P3, ..., PN and mass m uniformly distributed on its interior, rotating about an axis perpendicular to the plane and passing through the origin.

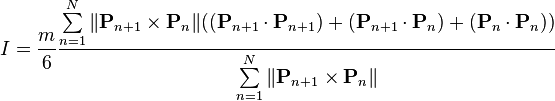
Plane regular polygon with n-vertices and mass m uniformly distributed on its interior, rotating about an axis perpendicular to the plane and passing through the origin. a stands for side length.
![I=\frac{ma^2}{24}[1 + 3\cot^2(\tfrac{\pi}{n})]](http://upload.wikimedia.org/math/6/c/d/6cd76c9be35e5f277cba4721eacf7606.png) [5]
[5]
Infinite disk with mass normally distributed on two axes around the axis of rotation with mass-density as a function of x and y:

Uniform disk about an axis perpendicular to its edge.
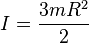 [6]
[6]
To obtain the scalar moments of inertia I above, the tensor moment of inertia I is projected along some axis defined by a unit vector n according to the formula:
Solid sphere of radius r and mass m

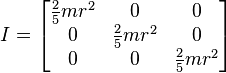
Hollow sphere of radius r and mass m


Solid ellipsoid of semi-axes a, b, c and mass m

Right circular cone with radius r, height h and mass m, about the apex


Solid cuboid of width w, height h, depth d, and mass m

Slender rod along y-axis of length l and mass m about end

Slender rod along y-axis of length l and mass m about center

Solid cylinder of radius r, height h and mass m
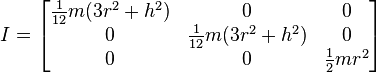
Thick-walled cylindrical tube with open ends, of inner radius r1, outer radius r2, length h and mass m


Description
Figure
Moment(s) of inertia
Point mass m at a distance r from the axis of rotation. A point mass does not have a moment of inertia around its own axis, but using the parallel axis theorem a moment of inertia around a distant axis of rotation is achieved.


Two point masses, M and m, with reduced mass μ and separated by a distance, x.

Rod of length L and mass m, axis of rotation at the end of the rod. This expression assumes that the rod is an infinitely thin (but rigid) wire. This is also a special case of the thin rectangular plate with axis of rotation at the end of the plate, with h = L and w = 0.

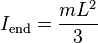 [1]
[1]Rod of length L and mass m. This expression assumes that the rod is an infinitely thin (but rigid) wire. This is a special case of the thin rectangular plate with axis of rotation at the center of the plate, with w = L and h = 0.

 [1]
[1]Thin circular hoop of radius r and mass m. This is a special case of a torus for b = 0 (see below), as well as of a thick-walled cylindrical tube with open ends, with r1 = r2 and h = 0.



Thin, solid disk of radius r and mass m. This is a special case of the solid cylinder, with h = 0. That
 is a consequence of the Perpendicular axis theorem.
is a consequence of the Perpendicular axis theorem.
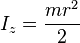

Thin cylindrical shell with open ends, of radius r and mass m. This expression assumes that the shell thickness is negligible. It is a special case of the thick-walled cylindrical tube for r1 = r2.
Also, a point mass m at the end of a rod of length r has this same moment of inertia and the value r is called the radius of gyration.

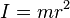 [1]
[1]Solid cylinder of radius r, height h and mass m.
This is a special case of the thick-walled cylindrical tube, with r1 = 0. (Note: X-Y axis should be swapped for a standard right handed frame).

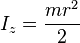 [1]
[1]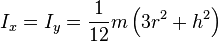
Thick-walled cylindrical tube with open ends, of inner radius r1, outer radius r2, length h and mass m. With a density of ρ and the same geometry
 ,
, 

 [1] [2]
[1] [2]where t = (r2–r1)/r2 is a normalized thickness ratio;
![I_x = I_y = \frac{1}{12} m\left[3\left({r_2}^2 + {r_1}^2\right)+h^2\right]](http://upload.wikimedia.org/math/3/b/2/3b287e5226f4bb01de7a7a3066f4202a.png)
Tetrahedron of side s and mass m


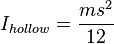
Octahedron (hollow) of side s and mass m


Octahedron (solid) of side s and mass m


Sphere (hollow) of radius r and mass m. A hollow sphere can be taken to be made up of two stacks of infinitesimally thin, circular hoops, where the radius differs from 0 to r (or a single stack, where the radius differs from -r to r).

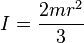 [1]
[1]Ball (solid) of radius r and mass m. A sphere can be taken to be made up of two stacks of infinitesimally thin, solid discs, where the radius differs from 0 to r (or a single stack, where the radius differs from -r to r).

 [1]
[1]Sphere (shell) of radius r2, with centered spherical cavity of radius r1 and mass m. When the cavity radius r1 = 0, the object is a solid ball (above).
When r1 = r2,
![\left[\frac{{r_2}^5-{r_1}^5}{{r_2}^3-{r_1}^3}\right]=\frac{5}{3}{r_2}^2](http://upload.wikimedia.org/math/d/5/7/d57cd8acd84d2fac233b03050dd61fac.png) , and the object is a hollow sphere.
, and the object is a hollow sphere.
![I = \frac{2 m}{5}\left[\frac{{r_2}^5-{r_1}^5}{{r_2}^3-{r_1}^3}\right]\,\!](http://upload.wikimedia.org/math/d/7/3/d7341dbed710e5dd97ef720c6f2582db.png) [1]
[1]Right circular cone with radius r, height h and mass m

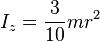 [3]
[3] [3]
[3]Torus of tube radius a, cross-sectional radius b and mass m.

About the vertical axis:
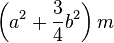 [4]
[4]About a diameter:
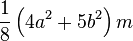 [4]
[4]Ellipsoid (solid) of semiaxes a, b, and c with mass m




Thin rectangular plate of height h, width w and mass m
(Axis of rotation at the end of the plate)


Thin rectangular plate of height h and of width w and mass m

 [1]
[1]Solid cuboid of height h, width w, and depth d, and mass m. For a similarly oriented cube with sides of length
 ,
, 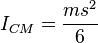

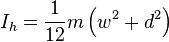
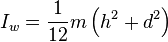
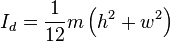
Solid cuboid of height D, width W, and length L, and mass m with the longest diagonal as the axis. For a cube with sides
 ,
,  .
.

Triangle with vertices at the origin and at P and Q, with mass m, rotating about an axis perpendicular to the plane and passing through the origin.

Plane polygon with vertices P1, P2, P3, ..., PN and mass m uniformly distributed on its interior, rotating about an axis perpendicular to the plane and passing through the origin.

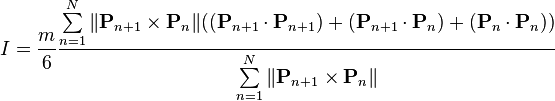
Plane regular polygon with n-vertices and mass m uniformly distributed on its interior, rotating about an axis perpendicular to the plane and passing through the origin. a stands for side length.
![I=\frac{ma^2}{24}[1 + 3\cot^2(\tfrac{\pi}{n})]](http://upload.wikimedia.org/math/6/c/d/6cd76c9be35e5f277cba4721eacf7606.png) [5]
[5]Infinite disk with mass normally distributed on two axes around the axis of rotation with mass-density as a function of x and y:


Uniform disk about an axis perpendicular to its edge.
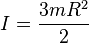 [6]
[6]List of 3D inertia tensors
This list of moment of inertia tensors is given for principal axes of each object.To obtain the scalar moments of inertia I above, the tensor moment of inertia I is projected along some axis defined by a unit vector n according to the formula:
Solid sphere of radius r and mass m

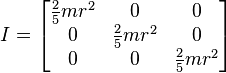
Hollow sphere of radius r and mass m


Solid ellipsoid of semi-axes a, b, c and mass m


Right circular cone with radius r, height h and mass m, about the apex


Solid cuboid of width w, height h, depth d, and mass m

Slender rod along y-axis of length l and mass m about end

Slender rod along y-axis of length l and mass m about center

Solid cylinder of radius r, height h and mass m

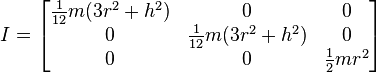
Thick-walled cylindrical tube with open ends, of inner radius r1, outer radius r2, length h and mass m


| Description | Figure | Moment of inertia tensor |
|---|




No comments:
Post a Comment