ⶌⶌⶌ Fast Romantics: April 2015

Wednesday, April 15, 2015

Moments of inertia

Following are scalar moments of inertia. In general, the moment of inertia is a tensor, see below.

Description
Figure
Moment(s) of inertia

Point mass m at a distance r from the axis of rotation. A point mass does not have a moment of inertia around its own axis, but using the parallel axis theorem a moment of inertia around a distant axis of rotation is achieved.

Two point masses, M and m, with reduced mass μ and separated by a distance, x.
$I = \frac{ M m }{ M \! + \! m } x^2 = \mu x^2$

Rod of length L and mass m, axis of rotation at the end of the rod. This expression assumes that the rod is an infinitely thin (but rigid) wire. This is also a special case of the thin rectangular plate with axis of rotation at the end of the plate, with h = L and w = 0.

$I_{\mathrm{end}} = \frac{m L^2}{3} \,\!$ ^[1]

Rod of length L and mass m. This expression assumes that the rod is an infinitely thin (but rigid) wire. This is a special case of the thin rectangular plate with axis of rotation at the center of the plate, with w = L and h = 0.

$I_{\mathrm{center}} = \frac{m L^2}{12} \,\!$ ^[1]

Thin circular hoop of radius r and mass m. This is a special case of a torus for b = 0 (see below), as well as of a thick-walled cylindrical tube with open ends, with r₁ = r₂ and h = 0.

$I_z = m r^2\!$
$I_x = I_y = \frac{m r^2}{2}\,\!$

Thin, solid disk of radius r and mass m. This is a special case of the solid cylinder, with h = 0. That $I_x = I_y = \frac{I_z}{2}\,$ is a consequence of the Perpendicular axis theorem.

$I_z = \frac{m r^2}{2}\,\!$
$I_x = I_y = \frac{m r^2}{4}\,\!$

Thin cylindrical shell with open ends, of radius r and mass m. This expression assumes that the shell thickness is negligible. It is a special case of the thick-walled cylindrical tube for r₁ = r₂.
Also, a point mass m at the end of a rod of length r has this same moment of inertia and the value r is called the radius of gyration.

$I = m r^2 \,\!$ ^[1]

Solid cylinder of radius r, height h and mass m.
This is a special case of the thick-walled cylindrical tube, with r₁ = 0. (Note: X-Y axis should be swapped for a standard right handed frame).

$I_z = \frac{m r^2}{2}\,\!$ ^[1]
$I_x = I_y = \frac{1}{12} m\left(3r^2+h^2\right)$

Thick-walled cylindrical tube with open ends, of inner radius r₁, outer radius r₂, length h and mass m. With a density of ρ and the same geometry $I_z = \frac{1}{2} \pi\rho h\left({r_2}^4 - {r_1}^4\right)$ , $I_x = I_y = \frac{1}{12} \pi\rho h\left(3({r_2}^4 - {r_1}^4)+h^2({r_2}^2 - {r_1}^2)\right)$

$I_z = \frac{1}{2} m\left(r_1^2 + r_2^2\right) = m r_2^2 \left(1-t+\frac{1}{2}{t}^2\right)$ ^[1] ^[2]
where t = (r₂–r₁)/r₂ is a normalized thickness ratio;
$I_x = I_y = \frac{1}{12} m\left[3\left({r_2}^2 + {r_1}^2\right)+h^2\right]$

Tetrahedron of side s and mass m

$I_{solid} = \frac{m s^2}{20}\,\!$ $I_{hollow} = \frac{m s^2}{12}\,\!$

Octahedron (hollow) of side s and mass m

$I_z=I_x=I_y = \frac{5m s^2}{9}\,\!$

Octahedron (solid) of side s and mass m

$I_z=I_x=I_y = \frac{m s^2}{5}\,\!$

Sphere (hollow) of radius r and mass m. A hollow sphere can be taken to be made up of two stacks of infinitesimally thin, circular hoops, where the radius differs from 0 to r (or a single stack, where the radius differs from -r to r).

$I = \frac{2 m r^2}{3}\,\!$ ^[1]

Ball (solid) of radius r and mass m. A sphere can be taken to be made up of two stacks of infinitesimally thin, solid discs, where the radius differs from 0 to r (or a single stack, where the radius differs from -r to r).

$I = \frac{2 m r^2}{5}\,\!$ ^[1]

Sphere (shell) of radius r₂, with centered spherical cavity of radius r₁ and mass m. When the cavity radius r₁ = 0, the object is a solid ball (above).
When r₁ = r₂, $\left[\frac{{r_2}^5-{r_1}^5}{{r_2}^3-{r_1}^3}\right]=\frac{5}{3}{r_2}^2$ , and the object is a hollow sphere.

$I = \frac{2 m}{5}\left[\frac{{r_2}^5-{r_1}^5}{{r_2}^3-{r_1}^3}\right]\,\!$ ^[1]

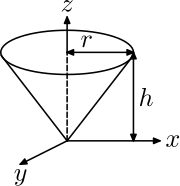
Right circular cone with radius r, height h and mass m

$I_z = \frac{3}{10}mr^2 \,\!$ ^[3]
$I_x = I_y = \frac{3}{5}m\left(\frac{r^2}{4}+h^2\right) \,\!$ ^[3]

Torus of tube radius a, cross-sectional radius b and mass m.

About the vertical axis: $\left(a^2 + \frac{3}{4}b^2\right)m$ ^[4]
About a diameter: $\frac{1}{8}\left(4a^2 + 5b^2\right)m$ ^[4]

Ellipsoid (solid) of semiaxes a, b, and c with mass m

$I_a = \frac{m (b^2+c^2)}{5}\,\!$

$I_b = \frac{m (a^2+c^2)}{5}\,\!$

$I_c = \frac{m (a^2+b^2)}{5}\,\!$

Thin rectangular plate of height h, width w and mass m
(Axis of rotation at the end of the plate)

$I_e = \frac {m h^2}{3}+\frac {m w^2}{12}\,\!$

Thin rectangular plate of height h and of width w and mass m

$I_c = \frac {m(h^2 + w^2)}{12}\,\!$ ^[1]

Solid cuboid of height h, width w, and depth d, and mass m. For a similarly oriented cube with sides of length

, $I_{CM} = \frac{m s^2}{6}\,\!$

Moment of inertia solid rectangular prism.png

$I_h = \frac{1}{12} m\left(w^2+d^2\right)$
$I_w = \frac{1}{12} m\left(h^2+d^2\right)$
$I_d = \frac{1}{12} m\left(h^2+w^2\right)$

Solid cuboid of height D, width W, and length L, and mass m with the longest diagonal as the axis. For a cube with sides

, $I = \frac{m s^2}{6}\,\!$ .

$I = \frac{m\left(W^2D^2+L^2D^2+L^2W^2\right)}{6\left(L^2+W^2+D^2\right)}$

Triangle with vertices at the origin and at P and Q, with mass m, rotating about an axis perpendicular to the plane and passing through the origin.

$I=\frac{m}{6}(\mathbf{P}\cdot\mathbf{P}+\mathbf{P}\cdot\mathbf{Q}+\mathbf{Q}\cdot\mathbf{Q})$

Plane polygon with vertices P₁, P₂, P₃, ..., P_N and mass m uniformly distributed on its interior, rotating about an axis perpendicular to the plane and passing through the origin.

$I=\frac{m}{6}\frac{\sum\limits_{n=1}^{N}\|\mathbf{P}_{n+1}\times\mathbf{P}_{n}\|((\mathbf{P}_{n+1}\cdot\mathbf{P}_{n+1})+(\mathbf{P}_{n+1}\cdot\mathbf{P}_{n})+(\mathbf{P}_{n}\cdot\mathbf{P}_{n}))}{\sum\limits_{n=1}^{N}\|\mathbf{P}_{n+1}\times\mathbf{P}_{n}\|}$

Plane regular polygon with n-vertices and mass m uniformly distributed on its interior, rotating about an axis perpendicular to the plane and passing through the origin. a stands for side length.
$I=\frac{ma^2}{24}[1 + 3\cot^2(\tfrac{\pi}{n})]$ ^[5]

Infinite disk with mass normally distributed on two axes around the axis of rotation with mass-density as a function of x and y:

$\rho(x,y) = \tfrac{m}{2\pi ab}\, e^{-((x/a)^2+(y/b)^2)/2}\,,$

$I = m (a^2+b^2) \,\!$

Uniform disk about an axis perpendicular to its edge.
$I = \frac {3mR^2} {2}$ ^[6]

List of 3D inertia tensors

This list of moment of inertia tensors is given for principal axes of each object.
To obtain the scalar moments of inertia I above, the tensor moment of inertia I is projected along some axis defined by a unit vector n according to the formula:

$\mathbf{n}\cdot\mathbf{I}\cdot\mathbf{n}\equiv n_i I_{ij} n_j\,,$

where the dots indicate tensor contraction and we have used the Einstein summation convention. In the above table, n would be the unit Cartesian basis e_x, e_y, e_z to obtain I_x, I_y, I_z respectively.

Solid sphere of radius r and mass m

$I = \begin{bmatrix} \frac{2}{5} m r^2 & 0 & 0 \\ 0 & \frac{2}{5} m r^2 & 0 \\ 0 & 0 & \frac{2}{5} m r^2 \end{bmatrix}$

Hollow sphere of radius r and mass m

$I = \begin{bmatrix} \frac{2}{3} m r^2 & 0 & 0 \\ 0 & \frac{2}{3} m r^2 & 0 \\ 0 & 0 & \frac{2}{3} m r^2 \end{bmatrix}$

Solid ellipsoid of semi-axes a, b, c and mass m

$I = \begin{bmatrix} \frac{1}{5} m (b^2+c^2) & 0 & 0 \\ 0 & \frac{1}{5} m (a^2+c^2) & 0 \\ 0 & 0 & \frac{1}{5} m (a^2+b^2) \end{bmatrix}$

Right circular cone with radius r, height h and mass m, about the apex

$I = \begin{bmatrix} \frac{3}{5} m h^2 + \frac{3}{20} m r^2 & 0 & 0 \\ 0 & \frac{3}{5} m h^2 + \frac{3}{20} m r^2 & 0 \\ 0 & 0 & \frac{3}{10} m r^2 \end{bmatrix}$

Solid cuboid of width w, height h, depth d, and mass m

$I = \begin{bmatrix} \frac{1}{12} m (h^2 + d^2) & 0 & 0 \\ 0 & \frac{1}{12} m (w^2 + d^2) & 0 \\ 0 & 0 & \frac{1}{12} m (w^2 + h^2) \end{bmatrix}$

Slender rod along y-axis of length l and mass m about end

$I = \begin{bmatrix} \frac{1}{3} m l^2 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & \frac{1}{3} m l^2 \end{bmatrix}$

Slender rod along y-axis of length l and mass m about center

$I = \begin{bmatrix} \frac{1}{12} m l^2 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & \frac{1}{12} m l^2 \end{bmatrix}$

Solid cylinder of radius r, height h and mass m

$I = \begin{bmatrix} \frac{1}{12} m (3r^2+h^2) & 0 & 0 \\ 0 & \frac{1}{12} m (3r^2+h^2) & 0 \\ 0 & 0 & \frac{1}{2} m r^2\end{bmatrix}$

Thick-walled cylindrical tube with open ends, of inner radius r₁, outer radius r₂, length h and mass m

$I = \begin{bmatrix} \frac{1}{12} m (3({r_1}^2 + {r_2}^2)+h^2) & 0 & 0 \\ 0 & \frac{1}{12} m (3({r_1}^2 + {r_2}^2)+h^2) & 0 \\ 0 & 0 & \frac{1}{2} m ({r_1}^2 + {r_2}^2)\end{bmatrix}$

Description	Figure	Moment of inertia tensor

Pages

Wednesday, April 15, 2015

Moments of inertia

List of 3D inertia tensors